The Scallop Theorem basically says a swimmer needs to deform in a way that is not invariant under time-reversal. That’s some heady stuff.
Back in 1977, one Edward Mills Purcell, who shared the 1952 Nobel Prize for Physics, came up with that gem in a paper entitled Life at Low Reynolds Number, and in it he explained the physical principles of aquatic locomotion. It’s named for the scallop, which it so happens is the lone bivalve able to actively swim distances.
Unfortunately for the scallop, its technique doesn’t apply if it’s immersed in viscous fluids.
Amoebae are capable of swimming towards a chemical attractant by producing a thrust against a liquid medium to propel themselves with fluttering cilia, but the way scallops swim is a whole different kettle of fish. The Scallop Theorem explains it like this: a normal scallop moves by opening its shells slowly, and then rapidly shutting them. As a fluid between the shells is propelled outward from inside the shells, the resulting momentum of the water in motion pushes the scallop forward.
Seems logical, but Purcell understood that a microorganism trying to do the same thing would only move forward on shutting its shells – and then move back to its original position as they opened once more. So Purcell worked to suggest various ways which an organism could swim in thick fluids.
Now imagine a time when, provided scientists can understand how to overcome the Purcell problem, tiny structures like scallops or amoebae could be created which travel down blood vessels in search of blockages or tumors.
That moment may not be far off as a team of researchers have used 3D printing to create a “micro-scallop” of sub-millimeter size which might allow noninvasive exploration inside the human body.
Now the research team has published their findings in a paper entitled Swimming By Reciprocal Motion at Low Reynolds Number to describe how such a system might work.
The principal authors of the work, Tian Qiu, Tung-Chun Lee, Andrew G. Mark, and Peer Fischer of the Max Planck Institute for Intelligent Systems in Stuttgart, Germany, say that their work confirms that the tiny structure they designed, despite the Scallop Theorem, can generate propulsion.
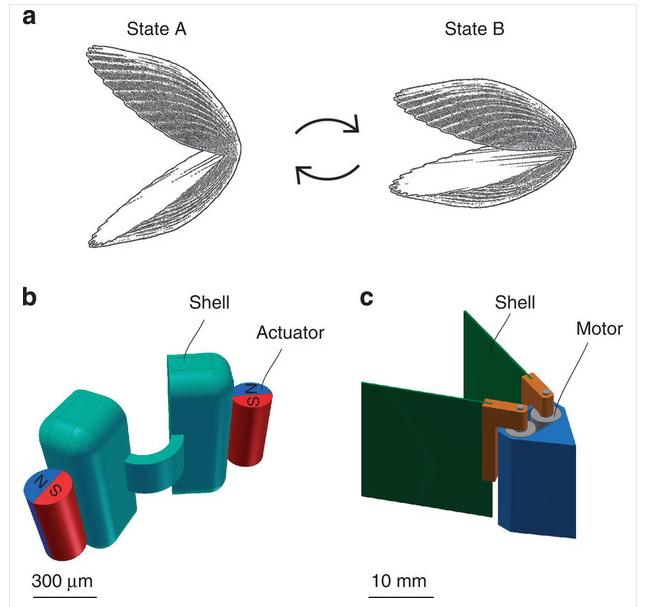
They did it by building a single-hinge, “micro-swimmer” that moves much like the scallop described by Purcell. These “micro-scallops” were made from polydimethylsiloxane (PDMS) and loaded with phosphorescent pigment before being cast into a 3D printed mold.
Each micro-scallop is made up of 300 μm shells connected by a 60 μm hinge, and rare earth micromagnets are then attached to each shell which can be reoriented. Once a magnetic field which drives the closing is decreased, the tension of the PDMS hinge opens the micro-scallop, and voila, motion in goo.
Watch a video of the 3D printed scallop in motion here (download).
What do you think about these tiny, swimming devices? Discuss in the How 3D Printed Micro-Scallops Might Travel in Our Blood thread on 3DPB.com.
