UK Researchers: Single-Droplet Resolution for 3D Printed Functional Synthetic Tissues

a Schematic of a pair of aqueous droplets forming a droplet interface bilayer (DIB) in a lipid-in-oil solution, and the definition of the equilibrium contact angle (θDIB). b–e Bright-field and fluorescence microscopy overlays of droplet pairs formed with 1 mM DPhPC and φSIL values of 0.20 (θDIB = 6.0 ± 0.7°) (b), 0.50 (θDIB = 26.5 ± 1.7°) (c), 0.80 (θDIB = 53.4 ± 0.8°) (d) and with 1 mM POPC and φSIL = 0.65 (θDIB = 85.3 ± 3.8°) (e). Scale bars = 150 µm. In each image, the right droplet contains 10 µM Atto488 to demonstrate that a bilayer has formed and compartmentalises the bilayer-impermeant dye. f A plot showing the linear dependence of θDIB with respect to φSIL for 1 mM DPhPC (linear regression R2 = 0.99) (see Supplementary Table 1). g A plot showing the linear dependence of θDIB with respect to xPOPC at φSIL = 0.65 (linear regression R2 = 0.99) (see Supplementary Table 2). h A plot of the 2D linear dependence of θDIB with respect to both φSIL and xPOPC (regression plane R2 = 0.99) (see Supplementary Table 8). The total lipid concentration was 1 mM. Data points that lie above and below the regression plane are in magenta and cyan, respectively. For all experiments, the aqueous phase was PBS at pH 7.2. Each data point in f–h is the mean of n > 3 contact angle measurements, and the error bars represent the standard deviation. When error bars are not visible, they have standard deviations smaller than the data symbols. (For individual n values, see Supplementary Table 24.)

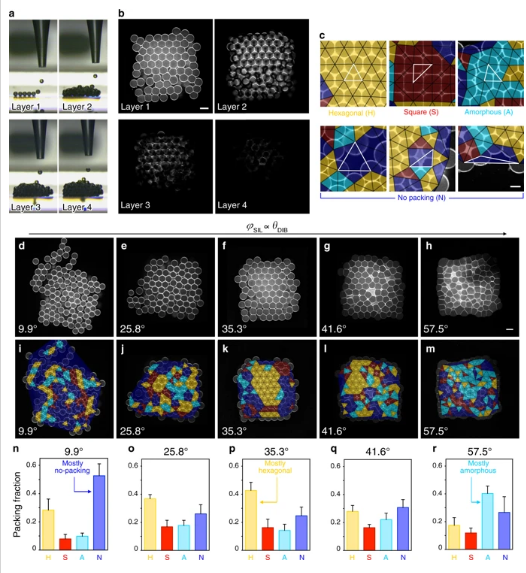
a Images of a 3D-printed droplet network (7 × 8 × 4 droplets in x, y and z directions) as each layer (1 to 4) is formed. b Horizontal cross-sections of layer 1 (bottom), layer 2, layer 3 and layer 4 of a droplet network imaged by confocal microscopy. Lipid bilayers and monolayers are visualized with Atto550M. c Examples of packing types in the first layer of 3D-printed networks. Our classification method draws triangles (indicated by black and highlighted white triangles) between the centers of three neighboring droplets and assigns the local packing type of each triplet based on the triangle geometry (Delaunay triangulation). Droplet triplets are classified as packed in a hexagonal (yellow), square (red) or amorphous (cyan) fashion, or not packed (blue) (see “Methods”). d–m Confocal microscopy images (d–h) and overlays of the packing analysis based on Delaunay triangulation (i–m) of the first layer of 3D-printed droplet networks at increasing φSIL values (corresponding to increasing θDIB). Yellow, red, cyan, and blue triangles represent the packing types defined as hexagonal, square, amorphous, and no packing, respectively. Scale bar = 100 µm. n–r Quantification of hexagonal (yellow), square (red), amorphous (cyan) and no-packing (blue) area fractions in the first layer of 3D-printed droplet networks at increasing values of φSIL. In n–r, each bar is the mean of n > 3 networks (see Supplementary Table 21 for individual n values and Supplementary Fig. 3); error bars represent the standard deviation.

For all conditions in a–e, θDIB = 36.3° (calculated from Eq. (1)). The φSIL and xPOPC values in b–d are φSIL = 0.60 and xPOPC = 0.00 (cyan), φSIL = 0.55 and xPOPC = 0.13 (purple), and φSIL = 0.52 and xPOPC = 0.20 (magenta). a Optical microscopy images of two droplets (75 nL) forming a DIB after contact. The non-equilibrium contact angle (θ) increases with time (0–900 s) until the equilibrium contact angle (θDIB) is reached (t = 1800 s). Scale bar = 150 µm. The images correspond to timepoints along the purple profile in b. b Plots of θ versus time for droplet pairs. Plots are the mean of n = 5 repeats for each condition, and error bars represent the standard deviation. The grey dashed lines correspond to timepoints relevant to printing 3D droplet networks: tfast (0.50 s), tdrop (2.00 s) and tslow (4.00 s) indicate the time intervals between consecutive printed droplets at fast (tfast−1 = 2.00 s−1), standard (tdrop−1 = 0.50 s−1), and slow (tslow−1 = 0.25 s−1) printing frequencies; tlayer (225 s) is the time it takes to print a single layer at a printing frequency of 0.50 s−1. c A bar chart of the hexagonal packing area fraction of 3D droplet networks printed at a droplet ejection frequency of 0.50 s−1. The hexagonal area fraction under the purple condition was significantly greater than for the other two conditions (one-way ANOVA with Tukey’s multiple comparison test) (see Supplementary Table 15). d Plots of hexagonal packing area fractions in the first layers of 3D droplet networks generated at different printing frequencies (fD). The frequencies marked in grey are the inverse of the timepoints marked in b (i.e., fD = tD−1, where tD is the time interval between the ejection of two consecutive droplets). For statistical tests, see Supplementary Table 16. e A confocal microscopy image and overlay of Delaunay triangulation of the first layer in a 3D-printed droplet network (7 × 8 × 4; x, y, z) at φSIL =  0.55 and xPOPC = 0.13 (purple condition in b–d) at a printing frequency of 0.50 s−1. Scale bar = 100 µm. Each data point in the graphs c and d is the mean of n > 3 repeats, and error bars represent the standard deviation. *, ** and *** indicate p-value <0.05, 0.01 and 0.001, respectively. For individual n values, see Supplementary Tables 22 and 23.

a–c Bright-field microscopy images of a 3D-printed droplet network (10 × 12 × 4; x, y, z) (1 mM DPhPC, φSIL = 0.60, and a calculated θDIB = 36.3° from Supplementary Fig. 5b) comprising an aqueous phase of 20% (w/v) poly(ethylene glycol) diacrylate, 0.5% (w/v) Irgacure 2959 (photo-initiator), 100 µM ethidium bromide-N,N’-bisacrylamide (photo-cross-linkable fluorophore), and PBS, before (a) and after (b) photo-polymerisation with UV light. Scale bars = 100 µm. c An image of an hcp cluster of hydrogel polyhedra dispersed in PBS. Scale bar = 25 µm. d 3D reconstruction of droplet shapes from confocal microscopy of the hcp region in c, which contained 14 clustered droplets (Supplementary Movie 1). e, f A computer model of a trapezo-rhombic dodecahedron—the space-filling polyhedron of hexagonal close packing—viewed from below (e) (compare the white box in d) and above (f). g–i A droplet sectioned through the z-axis from bottom to top, with (inset) computer models of trapezo-rhombic dodecahedra showing 2D sections of three-fold (g, i) and six-fold (h) symmetry.

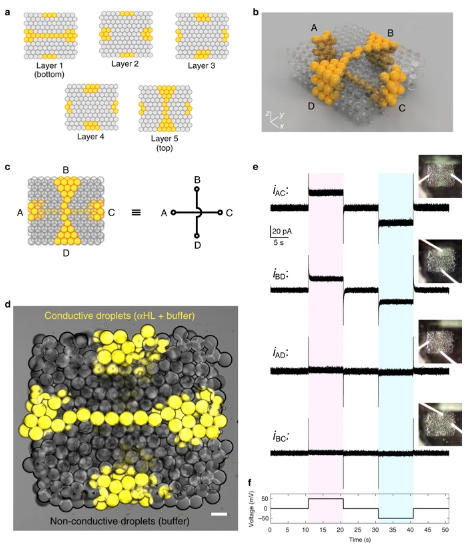
a Maps of the first (bottom), second, third, fourth and fifth (top) layers of a 3D-printed synthetic tissue in which two conductive, single-droplet-wide pathways containing αHL (in yellow) are patterned in 3D within a network of non-conductive droplets (in grey). b A computer model displaying the 3D architecture of the synthetic tissue. The two single-droplet-wide pathways span the synthetic tissue, one horizontally at the bottom (connecting A to C), and one vertically at the top (connecting B to D) of the network. c Simplified diagram of the synthetic tissue, and equivalent circuit model. d Bright-field and fluorescent microscopy overlay of the synthetic tissue. Droplets in the single-droplet-wide conductive pathways contained α-hemolysin (60 µg mL−1), 25 mM Tris-HCl (pH 7.6), 1 M NaCl and 10 µM Atto488 fluorophore (false coloured in yellow). Scale bar = 100 µm. e Electrical recordings of the ionic currents flowing through the two single-droplet-wide conductive pathways connecting A to C (iAC) and B to D (iBD) upon application of the voltage protocol shown in f. When a potential of ± 50 mV was applied, changes in ionic currents of +25.6 ± 1.4 pA (at positive potential) and −25.6 ± 1.5 pA (at negative potential) were observed for iAC, and of +19.4 ± 1.2 pA (at positive potential) and −19.8 ± 1.3 pA (at negative potential) for iBD. Conversely, we recorded non-significant changes in ionic current for the same applied potentials between A and D (iAD) or B and C (iBC). iAD: +1.8 ± 1.3 pA and −1.8 ± 1.4 pA (at positive and negative potentials respectively); iBC: +0.9 ± 1.1 pA and −0.9 ± 1.1 pA (at positive and negative potentials, respectively).