What is Metrology Part 22 – 3D Translation and Rotation

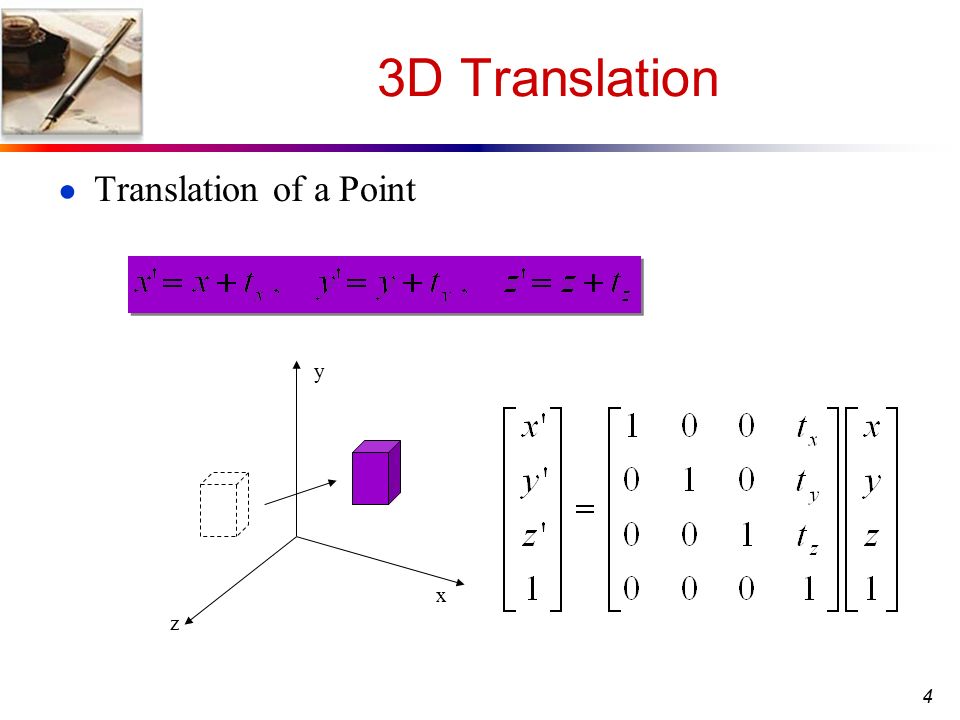
3D Translation

3D translation and rotation is vital within a 3D environment. We have discussed the importance of this within metrology previously in CMM systems. Interfacing the physical world and digital world requires precise measurement coordinates. Within 3D environments, movement is vital. In particular, movement is our focus today. We will talk about how example code within Processing can help us interface the digital world and physical realm. How does one simulate the real world within a virtual space? VR and 3D build environments are critical. So what are the basics needed for measurement and calculating space in a digital field? Metrology systems and laser scanning help. Tracking movement in terms of translation within a coordinate system is vital. So how could we learn about the basics of all of this? Let’s look into Processing as our main digital coding tool. How does Processing compute translational movement? If one wants to understand coding in a 3D environment, it is highly recommended that you understand object oriented program. We will not do a deep dive into this today, but a lot of the operations we are doing are object oriented. The following code is how I will demonstrate movement within Processing:

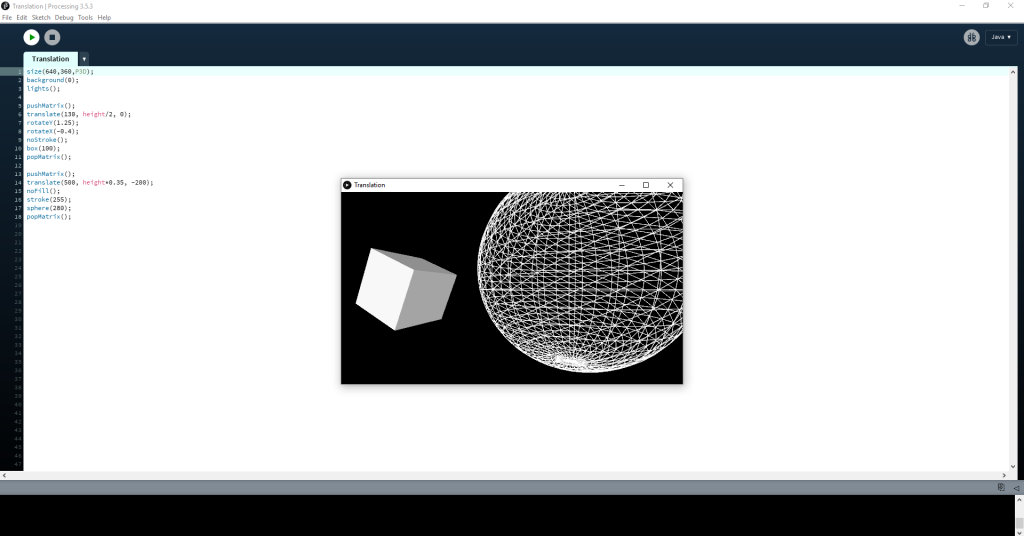
size(640,360,P3D);

background(0);

lights();

pushMatrix();

translate(130, height/2, 0);

rotateY(1.25);

rotateX(-0.4);

noStroke();

box(100);

popMatrix();

pushMatrix();

translate(500, height*0.35, -200);

noFill();

stroke(255);

sphere(280);

popMatrix();

Processing Example Code

Let’s take a look at this line by line. The first line is dedicated to building the 3D environment. The background of this window is denoted by the color value 0 which corresponds to black. The lights() function allows us to use ambient light, directional light, and specular values within our environment. In this case we are using the default light structure. pushMatrix(), we have discussed before as a function that allows us to set our original matrix of data that will be manipulated later. Our manipulation will come in the form of translational and rotational forces implemented. translate(130, height/2, 0) manipulation in question. The rotateY() function is used to move the window towards a particular angle based on units from the Y-axis of our viewport. The rotateX() function is similar except it is rotating within the X-axis. noStroke() allows us to be free from bordered 3D image renderings. box(100) allows us to create a 3D box with a float dimension of 100 in the x-dimension. popMatrix() ends the manipulation of the original data set. We then are able to start a new data manipulation through translation with pushMatrix(). This time, we have used the following command to apply a translation: translate(500, height*0.35, -200). Instead of a box though, we created a sphere for rotation.

Planar Rotation

We have focused a lot on coding basics within this metrology series as a whole. Being able to have standardized measuring devices within our metrology equipment is key. Without such, we would lack tangibility. If a 3D environment cannot be built with a computer, there is no way to interpret the data from a 3D world that we interact with. Being able to set a coordinate based on the world around us is still a difficult task though. So how can we do this? It makes us question how most of the devices we use in metrology are able to accurately set values of measurements based on the real world. These set of questions are things I would further like to explore.