3D Printed or Made by Hand: Models of Math Give Form to Equations

Many people don’t realize that math’s pages of equations have 3 dimensional counterparts and even fewer realize just how beautiful those forms can be. MIT has a series of such models on display that were created by the mathematician Felix Klein and his assistants. The complex forms that are dictated by these advanced equations were made into a series of models by building up a series of layers, in much the same way as a 3D printer builds up any other form. The difference here being that these models were built by hand over a century ago.

Klein and his team built the forms by first drawing horizontal sections of the planar form of the equations. Each one of these layers was cast separately in a powdered chalk plaster and then the layers were stacked together and glued in place until finally the complete body of the equation was born. Then, the creations were sanded and had lines etched in black upon their surfaces to demonstrate the principles of the particular equation.

For example, one of the models in the MIT collection illustrates what is known most commonly as the Clebsch Diagonal Cubic Surface. Interestingly, the alternate name for this equation is Klein’s Icosahedral Cubic Surface – named for the same Klein who created the models because of his contribution to the understanding of particular aspects of the surface. This is a cubic algebraic surface in which all 27 of the complex lines present on a general smooth cubic surface are real. In addition, 3 of the 27 lines meet at 10 points on the surface, and this is the only cubic surface on which that occurs.

This is more than just an abstract exercise. Creating 3 dimensional models of mathematical concepts provides an additional way of examining them and it can also serve to make them more accessible at a variety of levels. When it becomes possible for a student of mathematics to hold the results of an equation in their hands, and to play with it, aspects of the mechanics of math can become clearer and new questions can arise. This is true whether the form is a cube that has been handed to a first grader or a Clebsch Diagonal to a graduate student. These models, and others like them, are beautiful illustrations of the power of linking 2 dimensional instructions to 3 dimensional ideas.

These models can now be created much more easily with 3D modeling and printing technology. Klein was no sluggard just because he had to make by hand, or at least he had plenty of assistants, as there are a number of his chalk powder plaster models in the collections at MIT, University of Arizona, Harvard, and the University of Illinois at Urbana-Champaign.

There are a number of mathematical ideas that have as yet defied the magic of 3D printing and serve as the next frontier in 3D capabilities. One in particular, a postulate regarding the existence of hyperbolic space (a type of space in which the possibilities for the number of parallel lines that can exist on a surface is set at infinite) requires a shape that, as of yet, has only been possible to create through crochet. The idea behind this non-Euclidean theory was once believed to be an impossibility, but through it’s modeling in 3D space using crochet (which is simply another additive manufacturing technique, albeit one that is exclusive to hand-making) it has been acknowledged as valid.

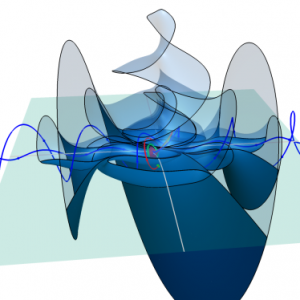
Exploring the possibilities for mathematics provided through 3D printing can help us to further our understanding of such complex forms such as the Calabi-Yau manifold which may actually be key to understanding the number and shape of the dimensions of space-time present in the universe. Other 3D versions of ideas such as Lorentzian Manifolds (see the computer model and hand crocheted version in the images above) present themselves for 3D printed exploration.

The power for advances in 3D technologies to make math more accessible through giving it physical form is one that holds great potential in education and advanced research. These technologies may not make the discoveries for us, but they certainly present them in a light that may make them easier to see.

Discuss this emerging application for 3D printing in the Math and 3D printing forum thread on 3DPB.com.